 The Multiplicative Group Is Cyclic
Now, every extension over F is a set of zeroes of the equation f(x):
| |
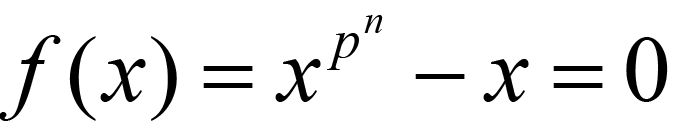 |
(1.1) |
and repeated products of the element x reveal that the multiplicative group is generated by x and so therefore is cyclic. (The zeroes of the above are all distinct.)
It also follows that every subgroup of a cyclic group is cyclic, so the multiplicative groups of every subfield of every extension field are also cyclic.
Then it is an observation that the Frobenius map (f(x)=xp) applied m times for some m|n will hold fixed a subfield of order pm in the extension of order pn.
It is not hard to reconcile the irreducible irr(x) with which the field is constructed with the formula (1.1) above. This is actually best done with inspecting Rabin's irreducibility test; which states that every maximal proper subfield of GF(p,n) has its multiplicative subgroup formed of the roots of some equation r(x) of the form
| |
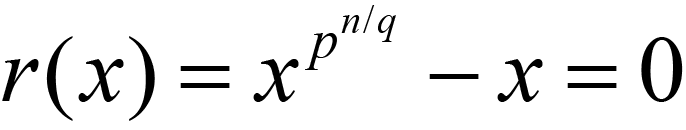 |
(1.2) |
Where q is any prime divisor of n (not a prime of greater power).
And the test stipulates that the gcd of an irreducible irr(x) and every form of equation (1.2) should be 1 and only 1. (I.e. the gcd=1 for all such primes q | n. There will always be a common root, but only the unity for a true irreducible.) And of course the test requires that the irreducible irr(x) must always divide f(x), the equation (1.1).
Then crucially the irreducible irr(x) will not factor into polynomials of lesser degree than itself with coefficients in any subfield of F[x] / <irr(x)>. If p(x) was such an irreducible factor then as irr(x) divides f(x) then p(x) of degree r would also divide f(x), and as every root of f(x) forms (generates) a cyclic group, one within which every subgroup itself is cyclic, it simply follows that p(x) (an irreducible over F) must divide some equation j(x) of the form:
| |
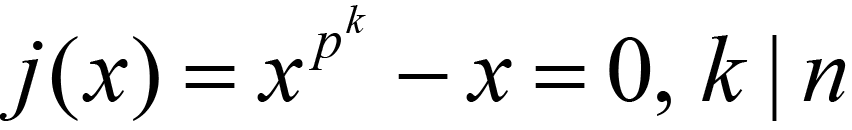 |
(1.3) |
Now, as k | n with k not equal to n, k must divide some n/q for q some prime power dividing n. (n splits into a factorisations of primes in the integers.)
So, any p(x) dividing irr(x) has a root that generates a cyclic subgroup of the group formed by the roots of the equation of the same form as j(x). Then
this root also generates a cyclic subgroup of that group of the form r(x) which contains the prior group. Hence, the gcd of p(x) and some equation as of r(x) will be of degree greater than one. I.e. as p(x) supposedly divides irr(x), then irr(x) would likewise have such a gcd with r(x) of degree > 1.
So, the gcd of irr(x) with some equation of the form r(x) must be unity for all q | n if irr(x) is irreducible. In the case that there exists some non-trivial p(x) | irr(x) then this test identifies the irreducible.
Also, crucially irr(x) must divide f(x)) for the roots of irr(x) to generate our extension. crucially the gcd of irr(x) with f(x) must be irr(x). i.e. irr(x) | f(x).
Now, All along I assumed that irr(x) divided f(x). I must show that if irr(x) does not divide f(x) then the test states irr(x) is not irreducible
The counter-intuitive part is that if irr(x) has a factor of degree r and r | n then irr(x) | f(x) and the above test applies. Else, if irr(x) has a factor of degree r with r not dividing n, then irr(x) does not divide f(x). This is not a problem, as irr(x) then has a non-trivial factor and is not irreducible.
Clearly, if r | n then p(x) | irr(x) shows p(x) of degree r contains a root which generates a subgroup of that field whose elements are roots of some particular equation r(x). The converse, when r does not divide n shows that p(x) of degree r does not divide f(x).
Why?
Case 1) g(x) | f(x)
Clearly (without loss of generality) we may reduce to the case where p(x) is not irredicible but has an irreducible factor g(x) of degree r < n.
Then I must show there is a finite field J of degree r over F that is a subfield of the field of degree n over F (our K). Then for an irreducible g(x), the subfield formed must be of degree r | n over F.
Now, if g(x) | f(x) then g(x) is formed of linear factors dividing f(x)=0. (As these are all linear and irreducible).
As g(x) may be considered irreducible (by induction hypophesis) There is a subfield F[x]/<g(x)> = J over F, and I must show g(x) divides f(x) if and only if J is a subfield of K.
If g(x) were not irreducible, as it divides f(x) it would yet split into irreducible factors over K; and so because g(x) | f(x), f(x) would contain the roots (all the factors) of g(x) and those of some irreducible h(x) dividing both g(x) and f(x), and there would be some field J in K that would suffice for induction.
So, as every root of our irreducible g(x) is a root of f(x). I state that there exists F[x] / <g(x)> = J a subfield of K (J < K), as K contains the closure of every sum and product of those roots in g(x) which are also roots of f(x), as within the set of all elements of K. g(x) is square-free as it divides f(x) which is also square free. (I.e. as from before the previous page). Then the subfield J of K which has it's characteristic polynomial j(x) (c.f. equation (1.3)) is also square free. Then, properly J < K.
I.e. every monic irreducible polynomial r(x) that completely splits into linear factors over K has degree r | n. (There exists a subfield of K of degree r | n extended over F.)
Then g(x) divides both f(x) and j(x) where j(x) is of the same form as equation (1.3) above, yet corresponding to J < K. Where J= F[x] / <g(x)>
So f(x) is the product of all monic irreducible polynomials g(x) of all degrees r | n. (and we know from the previous page these roots in any finite field J (or K) are square-free.) This is how best to relate the two polynomials f(x) and irr(x). f(x) is the least common multiple of all the monic irreducible polynomials of degree r | n.
Then, as every irreducible of degree r over F dividing f(x) corresponds to a field J < K over F, we may state that some irreducible factor h(x) of both j(x) and f(x) satisfies h(x) | gcd(j(x), f(x)), (As before, the equation f(x) corresponds to that of K in (1.1).)
Yet for every J which is a subfield of K, r | n and j(x) = gcd(j(x), f(x)). So every such irreducible g(x) = h(x) and then g(x) | j(x). and g(x) | f(x).
Then g(x) = h(x) divides gcd(j(x), f(x)) being irreducible and then dividing both f(x) and j(x).
Now, if g(x) is not irreducible then F[x] / <g(x)> forms no field and we may by induction reduce to some h(x) | g(x) etc which in fact is irreducible. The existence of such a subfield J for every irreducible ensures that r | n for all monic irreducible polynomials g(x) of degree r that divide our p(x) and f(x). Thus r | n by induction.
Else, as from division (g(x) / h(x)) | f(x) I repeat my induction until I show that every irreducible factor of g(x) dividing f(x), forms a subfield of K of degree r | n over F. Then, every root of g(x) (or indeed p(x)) is not just square-free but contained within a subfield of K.
If r does not divide n, then g(x) can not divide f(x).
Case 2) Conversely, if r | n
I note that equation (1.3) or j(x) divides f(x) when k | n. Considering the field J of pk elements, J is a subfield of K over F, K, the field of order pn elements. Mapping with a canonical morphism X from F[x] to J = F[x]/<g(x)> the kernel is formed by all polynomials divisible by g(x). Yet for every element in J, this satisfies f(x) =0 so the polynomial f(x) is in the kernel of the map X, and therefore g(x) | f(x).
So if equation (1.2) is as r(x) for all suitable primes dividing n, then, if p(x) | f(x) and gcd(p(x), r(x))) = 1 for all r(x) then p(x) is an irreducible over F of degree r = n. (Then p(x) | f(x) implies that r | n, but r does not divide any s that properly divides n so r = n.)
If g(x) does not divide f(x) then g(x) contains a factor which has degree r not dividing the degree n of f(x), so can not be irreducible. (Counter intuitive, but true).
If there is such an irreducible factor of g(x) of degree r not dividing n then there is an extension H over F that contains a subfield of degree r by induction. Then, g(x) which does not divide f(x) will certainly divide q(x) where q(x) is of the form (1.1) for a field of degree rn over F. (in fact, it will divide a q(x) for a field of degree lcm(r,n) over F.)
Then gcd(n, r) < n and there is a subfield J = F[x] / <g(x)> of degree gcd(n, r) over F which is a subfield of both K and H. Thus g(x) | gcd(f(x), q(x)) and if J is a subfield of K then r | n so gcd(n, r) = r.
Return To Section Start
Return To Previous Page |