That Induction Proof N(n,k)

I stated that the formula for the number of additive subgroups of the additive group of a finite field was given by the formula below.

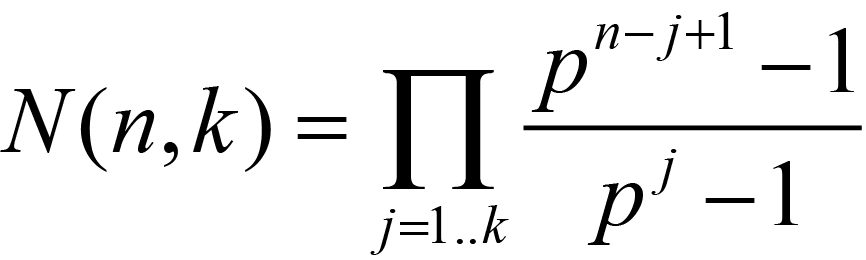
Where 'n' is the degree of the cartesian product of the prime subfield of F=GF(p,n) isomorphic to F+ and k is the dimension of the k-fold cartesian product of subgroups isomorphic to the prime subfield of F (which in a k-fold cartesian product form the "group" H in question). The number of such subgroups H of F+ that is given by the formula is exact.

We proceed by induction on k for a given n. I know the case k=1 is correct, as the number of additive groups is simply

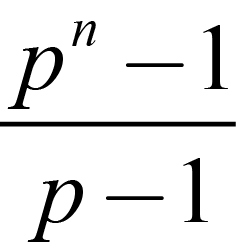(1.1)

Since each group is disjoint in elements except for the zero.

Now we start assuming that the case k-1 is correct and we obtain the desired result after a few calculations.

So, given a group H of order p^k-1 in G (of order pⁿ) every element not in H may extend the group to one of higher degree. These elements partition into their subgroups; as the extensions that may be possible are similar for every element of each p-order subgroup not in H. So the number of ways I may extend H to some group in G; (each a subgroup K_i) of order p^k is in part given by the formula:

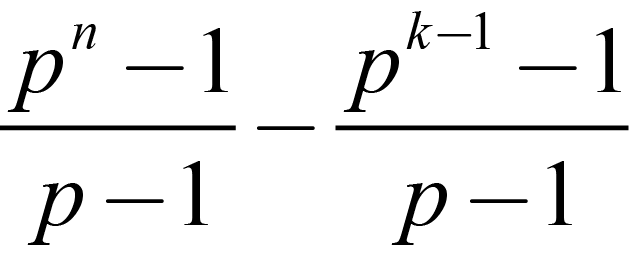(1.2)

Which simplifies to:

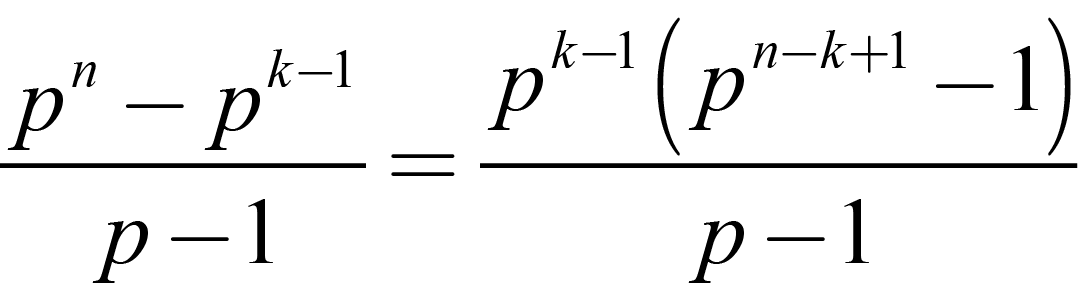(1.3)

Yet each one of these possible extensions are not unique: for in the extension of order p^k there are some few elements in every K_i which generate this group K_i not in H, i.e. these elements are in the set K \ H, (otherwise stated as K - H) the number of extensions formed is given by the number of the disjoint p-groups in K \ H which is given by:

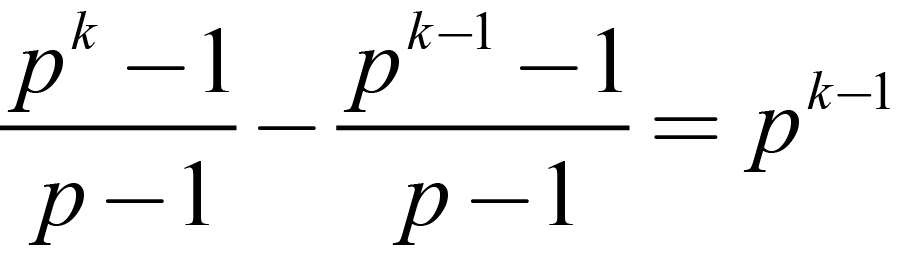(1.4)

Now, this is the number of p^k subgroups generated by each of the p^k-1 subgroups. Yet this is too many as each extension to a p^k group is made by more than one p^k-1 group.

So; (1.2) and (1.4) together simplify the count to:

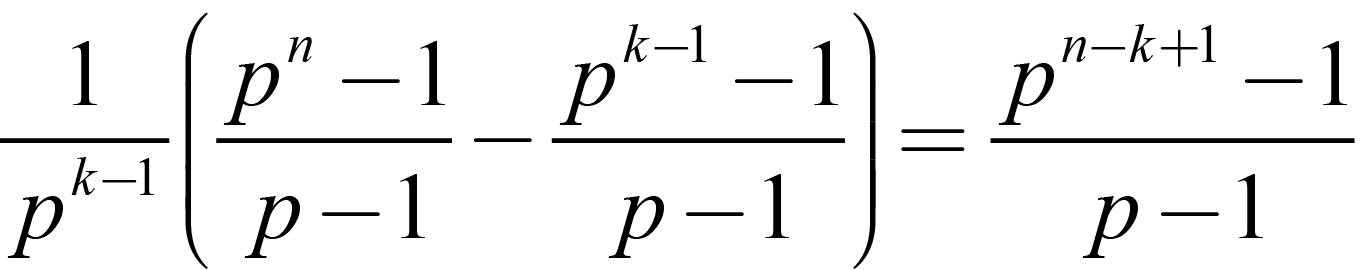(1.5)

And this gives us the number of individual groups K_i of order p^k generated by each of (but not unique to) each p^k-1 subgroup H extended to a K_i, one of order p^k (a subgroup isomorphic to K). Yet each p^k group or K_i may very well be generated by several of the p^k-1 groups isomorphic to H from the full collection of N(n, k-1). Fortunately, the number of p^k-1 groups in each p^k group K_i is the same as the number of unique factors of order p in each p^k group (see * at bottom). Then, by applying the p^k case, the number of unique subgroups is given by

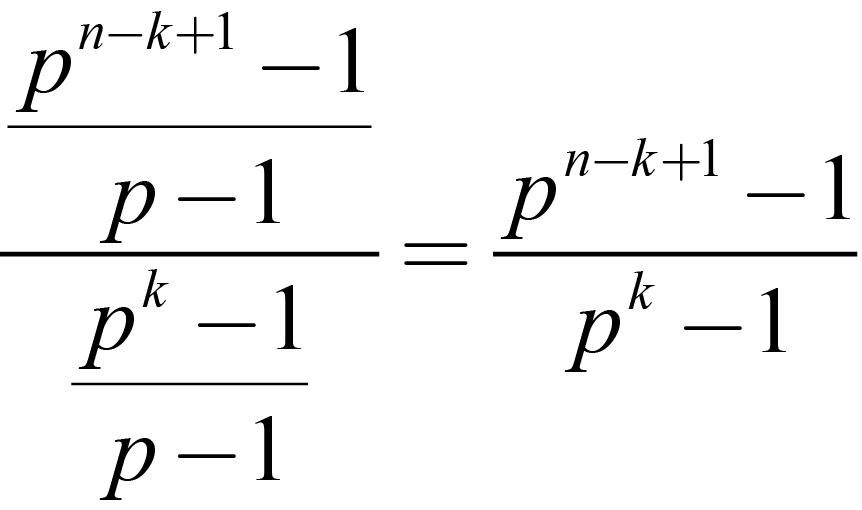(1.6)

And this is the multiple upon the number of such H; (our formula N(n, k-1)) which is truly the number of p^k subgroups of F.

Thus:

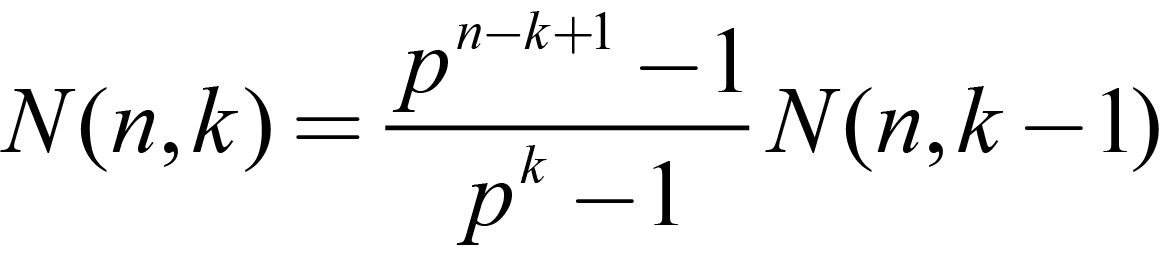(1.7)

And by counting backward to the case k=1

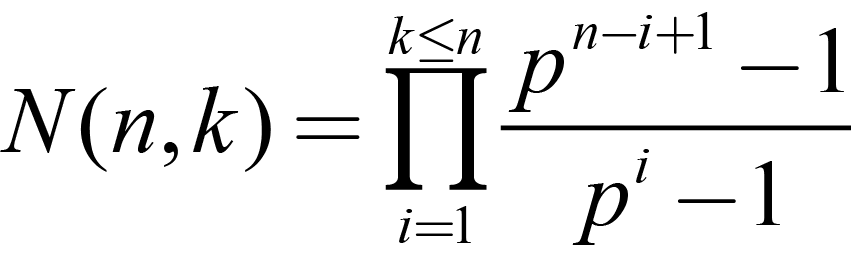(1.8)

Which was what was wanted.

*How could this be otherwise? Given the formula for the number of subgroups N(n, k) it is truly symmetrical in that N(n, k) = N(n, n-k). Indeed we simply apply the formula in the lesser case where N(k, 1) = N(k, k-1). Our induction hypothesis can be modified to account for this! We may state that for all n > 0, and subsequently all 0 < k < n the induction hypothesis shows that the formula N(n, k) is exact.

Then to prove p(n) we assume only p(k) for 0 < k < n; and the number of subgroups are calculated by simply "counting N(n, k) backwards" from k to 1 as in equation (1.7).

(The case N(n, n) = 1 is trivial, and so the induction hypothesis suffers no trouble.)

Thus, the number of p^k-1 groups that generate the very same p^k group is the same as the number of p-group factors (my Z) in the p^k group. The converse, that if two p^k-1 groups are equal and the p-group factor changes is simply given by the formula (1.4)

Do we have equality from (1.7)? We could state that:

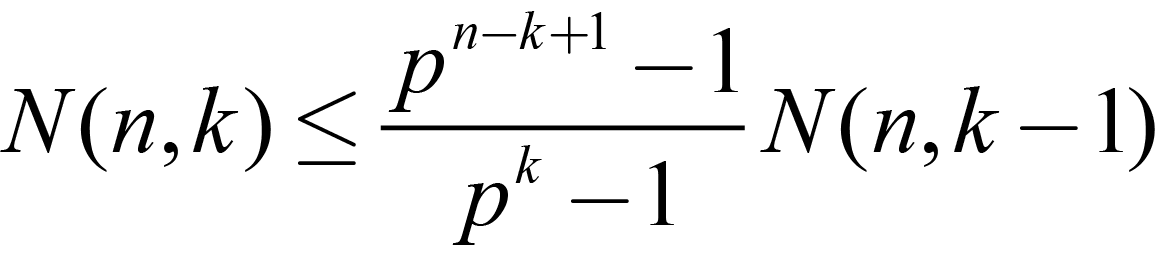(1.9)

Yet we do not rely on each p^k group in N(n,k) being uniquely generated by one p^k-1 group of N(n, k-1). Is it reasonable then to reduce the number by induction down from k=n-1 to k=1? I state that yes, it is and this is true by induction, as we are not finding the number of unique groups generated by each p^k-1 group H of the N(n, k-1) but are calculating the number of unique subgroups in the extension of the base p-group as a whole. The multiple is properly a “commensurate” or “ration” and is not a formula for the number of “unique” p^k groups so generated from each p^k-1 group.

Continue To Next Page

Return To Section Start